Edit 1: Added references to Neural Episodic Control + small section in the conclusions.
Edit 2: Disclaimer regarding what I mean by "DRL works".
You can use the BibTeX below if you would like to cite this post:
@misc{drlworksblog,
$\qquad$ title={Deep Reinforcement Learning Works - Now What?},
$\qquad$ author={Tessler, Chen},
$\qquad$ howpublished={\url{https://tesslerc.github.io/posts/drl_works_now_what/}},
$\qquad$ year={2020}
}
Two years ago, Alex Irpan wrote a post about why “Deep Reinforcement Learning Doesn’t Work Yet”. Since then, we have made huge algorithmic advances, tackling most of the problems raised by Alex. We have methods that are sample efficient [1, 21] and can learn in an off-policy batch setting [22, 23]. When lacking a reward function, we now have methods that can learn from preferences [24, 25] and even methods that are better fit to escape bad local extrema, when the return is non-convex [14, 26]. Moreover, we are now capable of training robust agents [27, 28] which can generalize to new and previously unseen domains!
Credits: https://openai.com/blog/solving-rubiks-cube/
Despite these advances, I argue that we, as a community, need to re-think several aspects. Below I highlight several fundamental problems, present some works which I believe are in the right direction and try to offer some plausible solutions.
* I’ll focus in this post on continuous control tasks, as this has been my main focus, but I believe that many of the insights and issues are relevant for discrete action spaces with visual inputs.
Disclaimer: each of us places a different threshold after which we allow ourselves to say that “Deep RL works”. As several years ago, solving tasks using RL (without any limitations) was a hard task, and the algorithms were very unstable, e.g., some seeds may succeed but many may utterly fail. Overcoming these pitfalls is my threshold, and as I see them, they no longer pose as major issues. Recent algorithmic improvements, combined with the ability to learn at extreme rates of parallelism, enable agents to consistently find good solutions to complex problems.
The Gap Between Theory and Practice
When it comes to the difference between theory and practice, there is a huge difference between the reinforcement and supervised learning communities. While in both communities there is a gap between what is theoretically guaranteed and analyzable, and what practitioners do, due to the sequential aspects of the RL task, I argue that in RL the theoretical and practical communities are much further apart and have much to learn from each other.
Direction 1) Practitioners have much to learn from the theoretical community. Often, the empirical community publish works which are in the right direction, but as they are unaware of the theoretical results/ignore them, the method is sub-optimal. We often see that fixing these methods, based on what is theoretically better, often works better in practice [31]. Moreover, in the empirical community practitioners often use inadequate models, such as stationary models for non-stationary MDPs, e.g., solve a finite horizon task like ATARI/MuJoCo using stationary models [30], and memory less models to solve POMDPs, such as sparse MuJoCo where the reward is accumulated across an entire trajectory and provided at the end [4].
Direction 2) Theoreticians have much to learn from the empirical community. When we compare the focuses of the theoretical and empirical communities, there is a mismatch in the directions each is proceeding. Take for instance the concept of total regret analysis [32], a scheme for quantifying the sub-optimality of the agent throughout the entire learning process. However, is this truly the objective we are interested in? There may be some scenarios in which the agent is run online and we wish to estimate regret, but I argue that for the most part, agents will be trained in a confined scenario and our true objective of interest is the simple regret (i.e., the agents performance after T timesteps) – the common objective in deep RL research [28, 33, 34, 35]! In addition, while analysis mostly focuses on count-based methods, in DRL we can’t count, but we can use Bayesian methods for uncertainty estimation, hence could Thompson sampling schemes may be a better fit [36].
I believe that by going hand in hand – analyzing what we observe to be empirically better and the practical use-cases, in addition to implementing and extending methods which are theoretically motivated – can push the RL community to new heights.
We’re Solving The Wrong Objective
I feel that one of the fundamental problems that plague the Deep RL (DRL) research community is the difference between what we aim to solve and what we solve in practice, and properly stating the differences and how this impacts our solution.
Two major examples are (1) solving the infinite horizon task and (2) regularization methods.
The Infinite Horizon
A common theme in DRL is to evaluate our agents on the finite horizon returns, i.e., how much reward our agent can obtain within T time-steps. This may indeed be our objective of interest, or maybe we are unable to properly estimate the performance in an “infinite horizon”. However, the reason doesn’t truly matter, this objective leads to a discrepancy between what our agents are trained to solve and what they solve in practice.
As the task has a finite horizon, the optimal policy is not necessarily stationary – it may depend on the time remaining. For instance, a basketball player will take fewer risks at the start of the game, but when there is 1 second left on the timer, clearly, he will throw the ball regardless of his location and odds of success. Practical DRL methods ignore this fact and focus on stationary models.
The basketball player throws (and in this case, scores) right before the game ends, an action which is strictly sub-optimal if the game had only begun.
While the task has a finite horizon (is played for at most T time-steps before receiving a timeout signal), our algorithms are incapable of maximizing the total undiscounted reward. As such, all works perform discounting. The objective has now changed, and as shown by Blackwell [13], when $\gamma$ isn’t close enough to $1$ (how close depends on the specific MDP), then the optimal policy for the $\gamma$-discounted task will not be identical to that of the total reward.
It seems that in the problems we currently solve, this scheme works relatively well, however, it is not clear what happens in real-world tasks, and in problems which are less repetitive than ATARI [16] and MuJoCo [17].
Regularization
RL is a hard problem, there is no denying this fact. And many methods use one form or another of regularization, whether knowingly or not, in order to stabilize things. For instance, in continuous control, a common scheme is to smooth the action-value function by adding noise to the policy [1, 14]. This is a form of exploration-consciousness [15], such that the agent is required to find the best policy which has a certain degree of randomness – while the optimal policy in this setting may be sub-optimal compared to the optimal deterministic policy, this is an easier problem to solve [20].
The above effect also happens when performing Q-learning with N-step returns. In this case, the Q value is computed by summing over N-1 steps in the experience replay, followed by bootstrapping the max value of the Nth state. As these transitions are off-policy, they contain the ε-exploration. For true estimates, the N-step return should be computed using a Tree Backup procedure [19]. However, practical methods utilize the data as-is [18], effectively including exploration and sub-optimal actions in the mix.
These methods aren’t wrong, they simply incorporate regularization in some form. But, it is important to consider how our objective changes when we apply one operator or another and to communicate these differences.
Hyper Parameters?
In previous work of mine [8, 10], I was very proud of the fact that we performed a hyperparameter sweep on a single domain. These parameters, combined with the proposed training process and loss were evaluated across multiple new domains, which were not used for parameter selection.
This may seem like a legitimate approach and obviously, we were not the first to do this [11 - before us, but also not the first]. However, this method prevents us from understanding the fundamental properties of the task.
For instance, consider the discount factor $\gamma$. When we tackle new environments and produce new algorithms, the common approach is to work with $\gamma = 0.99$. But why? Commonly, the goal is not to solve the $\gamma$-discounted infinite-horizon task, but rather $\gamma$ provides us with algorithmic stability. When then, should we select $\gamma = 0.99$?
It makes sense, that different algorithms and different environments would exhibit different behavior under varying discount factors. While one algorithm may enjoy improved stability due to $\gamma = 0.99$, for another it may hinder learning, such that a higher discount may be required, or a much smaller one. Moreover, different environments behave differently. A set of parameters optimal for one environment may be deemed strictly sub-optimal for another.
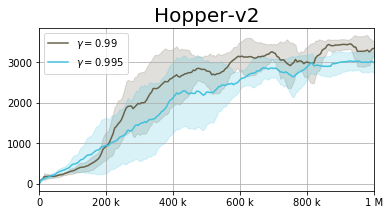
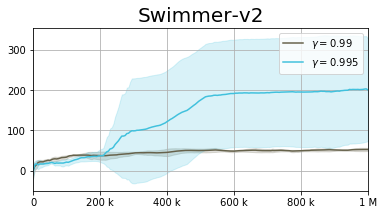
In addition to the figure above, we take a deeper look into the Hopper-v2 domain, analyzing how the performance changes as the discount factor varies.
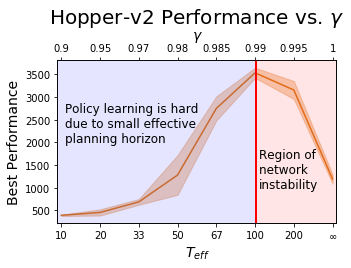
We observe two regions, which are algorithm and domain-dependent. The first is the well-known region of $\gamma < 0.99$, here, the effective planning horizon $T_{eff} = 1 / (1 - \gamma)$ is too low. As the agent is effectively planning for a short horizon it is incapable of properly solving the task. On the other hand, the more interesting region is at $\gamma > 0.99$. When the discount factor is too large, the algorithm suffers from instability, resulting in suboptimal performance.
Hence, as our goal is to maximize the performance in the MDP, the hyperparameters for each domain are simply another set of parameters for the RL algorithm to optimize, either manually or automatically [9].
Algorithm Novelty vs Performance
We as a community seem to admire either (1) SOTA performance or (2) complex algorithmic novelty. While these may be easier to evaluate as a reviewer, these do not necessarily drive the field forward. Often, the simpler method will not only have higher chances of community adoption, but also work better [1].
For instance, recent work has shown that, when performing robotic control from pixels, simple augmentation techniques combined with a simple policy learning algorithm outperform very complex previous algorithmic methods [37, 38].
This leads to a question as to what is the additional benefit of these complex methods? Does the algorithmic novelty truly result in a superior method, or does it impose some implicit bias/regularization on the learning process which in turn led to improved performance?
Lack of Simple Evaluation Environments
Deep RL has gone a long way since the DQN [7] was first introduced. There have been multiple advances along several fronts, yielding impressive results both in simulation and real life. Now that we have arrived at a point where we can proudly say “Deep RL does work”, I think we should take a step back and focus on the fundamentals.
By focusing on the fundamentals I do not necessarily mean tabular grid worlds, but on simple and analyzable domains from which we may derive meaningful conclusions about our algorithms. Most importantly, domains where we know what is the best possible reward. For instance, Humanoid-v2 has been long considered a complex task and previously reported results on the TD3 algorithm have shown it to utterly fail [13].
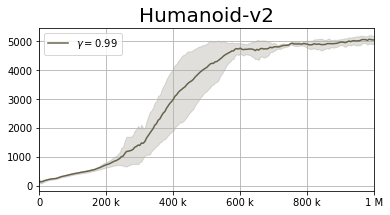
However, with a little hyper-parameter tuning we are capable of obtaining results which are competitive with the current SOTA. Are these results the best possible? Can existing algorithmic improvements take us further? Which algorithm is the best fit for continuous control tasks and why?
As each paper is incapable of performing precise parameter sweeps, and as there are many aspects such as weight initialization, network sizes, etc… It is not clear what role the various algorithmic improvements take. Do they truly improve our performance, or are the main benefits obtained by the additional tuning we perform in each paper? Currently, answering this question is of great importance, yet it isn’t easy. As we saw above, a very simple algorithm (TD3), combined with additional hyperparameter tuning, matches the performance of more complex methods such as OAC [29].
A proper understanding of the algorithms is crucial for proper advancement as a community. BSuite [6] provides several domains, in which we are capable of analytically calculating the optimal policy and thus compare metrics such as (1) simple regret and (2) total regret. While this does not yet include robotics domains, i.e., continuous action spaces, it enables the isolation of specific algorithmic properties that we would like to test. For instance, one domain may focus on non-stationarity while another on the hardness of exploration.
Closing Words
While I tried to highlight some issues I have encountered, and fallen for myself during my research; the state of DRL isn’t as bad as it used to be. We can proudly say that Deep RL does work, and there are many exciting lines of work that knowingly or not tackle the problems I have highlighted here.
An under-rated method is Evolution Strategies [2]. Also commonly referred to as random search, ES is capable of optimizing the real objective. By changing the policy, evaluating it on the total reward, and updating the weights based on the performance improvement, this scheme directly optimizes the policy with respect to the total reward.
Reward-Conditioned Policies [5] and Upside Down RL [3,4] convert the reinforcement learning problem into that of supervised learning. While many questions remain open (good for us! we can publish!), this line of work seems promising and may continue to surprise in the future, as supervised learning is a well-explored learning paradigm with many properties that RL can benefit from.
Finally, a line of work which I find super intriguing and hasn’t received enough attention is Neural Episodic Control [39]. Here, the authors provide a differentiable method for discretising the MDP. Their method provides both sample efficiency (due to the exact updates of the Q values) and reduces the need for certain hyper-parameters (reward clipping, discount factors, etc…).
It’s important to reflect back on what we have done, and what we can do better in the future. The fact that Deep RL does work enables us to take this step back and drive the field to new heights 💪.
Comment below!
Bibliography
[1] Fujimoto, Scott, Herke Hoof, and David Meger. “Addressing Function Approximation Error in Actor-Critic Methods.” International Conference on Machine Learning. 2018.
[2] Salimans, Tim, et al. “Evolution strategies as a scalable alternative to reinforcement learning.” arXiv preprint arXiv:1703.03864 (2017).
[3] Schmidhuber, Juergen. “Reinforcement Learning Upside Down: Don’t Predict Rewards–Just Map Them to Actions.” arXiv preprint arXiv:1912.02875 (2019).
[4] Srivastava, Rupesh Kumar, et al. “Training Agents using Upside-Down Reinforcement Learning.” arXiv preprint arXiv:1912.02877 (2019).
[5] Kumar, Aviral, Xue Bin Peng, and Sergey Levine. “Reward-Conditioned Policies.” arXiv preprint arXiv:1912.13465 (2019).
[6] Osband, Ian, et al. “Behaviour suite for reinforcement learning.” arXiv preprint arXiv:1908.03568 (2019).
[7] Mnih, Volodymyr, et al. “Human-level control through deep reinforcement learning.” Nature 518.7540 (2015): 529-533.
[8] Tessler, Chen, Daniel J. Mankowitz, and Shie Mannor. “Reward constrained policy optimization.” arXiv preprint arXiv:1805.11074 (2018).
[9] Xu, Zhongwen, Hado P. van Hasselt, and David Silver. “Meta-gradient reinforcement learning.” Advances in neural information processing systems. 2018.
[10] Tessler, Chen, Yonathan Efroni, and Shie Mannor. “Action Robust Reinforcement Learning and Applications in Continuous Control.” International Conference on Machine Learning. 2019.
[11] Schulman, John, et al. “Proximal policy optimization algorithms.” arXiv preprint arXiv:1707.06347 (2017).
[12] Blackwell, David. “Discrete dynamic programming.” The Annals of Mathematical Statistics (1962): 719-726.
[13] Haarnoja, Tuomas, et al. “Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor.” International Conference on Machine Learning. 2018.
[14] Tessler, Chen, Guy Tennenholtz, and Shie Mannor. “Distributional policy optimization: An alternative approach for continuous control.” Advances in Neural Information Processing Systems. 2019.
[15] Shani, Lior, Yonathan Efroni, and Shie Mannor. “Exploration Conscious Reinforcement Learning Revisited.” International Conference on Machine Learning. 2019.
[16] Bellemare, Marc G., et al. “The arcade learning environment: An evaluation platform for general agents.” Journal of Artificial Intelligence Research 47 (2013): 253-279.
[17] Todorov, Emanuel, Tom Erez, and Yuval Tassa. “Mujoco: A physics engine for model-based control.” 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2012.
[18] Hessel, Matteo, et al. “Rainbow: Combining improvements in deep reinforcement learning.” Thirty-Second AAAI Conference on Artificial Intelligence. 2018.
[19] Precup, Doina. “Eligibility traces for off-policy policy evaluation.” Computer Science Department Faculty Publication Series (2000): 80.
[20] Arumugam, Dilip, et al. “Mitigating planner overfitting in model-based reinforcement learning.” arXiv preprint arXiv:1812.01129 (2018).
[21] Cuccu, Giuseppe, Julian Togelius, and Philippe Cudré-Mauroux. “Playing atari with six neurons.” Proceedings of the 18th international conference on autonomous agents and multiagent systems. International Foundation for Autonomous Agents and Multiagent Systems, 2019.
[22] Fujimoto, Scott, David Meger, and Doina Precup. “Off-Policy Deep Reinforcement Learning without Exploration.” International Conference on Machine Learning. 2019.
[23] Kumar, Aviral, et al. “Stabilizing off-policy q-learning via bootstrapping error reduction.” Advances in Neural Information Processing Systems. 2019.
[24] Brown, Daniel, et al. “Extrapolating Beyond Suboptimal Demonstrations via Inverse Reinforcement Learning from Observations.” International Conference on Machine Learning. 2019.
[25] Christiano, Paul F., et al. “Deep reinforcement learning from human preferences.” Advances in Neural Information Processing Systems. 2017.
[26] Abdolmaleki, Abbas, et al. “Maximum a posteriori policy optimisation.” arXiv preprint arXiv:1806.06920 (2018).
[27] Peng, Xue Bin, et al. “Deepmimic: Example-guided deep reinforcement learning of physics-based character skills.” ACM Transactions on Graphics (TOG) 37.4 (2018): 1-14.
[28] Akkaya, Ilge, et al. “Solving Rubik’s Cube with a Robot Hand.” arXiv preprint arXiv:1910.07113 (2019).
[29] Ciosek, Kamil, et al. “Better Exploration with Optimistic Actor Critic.” Advances in Neural Information Processing Systems. 2019.
[30] Lillicrap, Timothy P., et al. “Continuous control with deep reinforcement learning.” International Conference on Learning Representations. 2016.
[31] Choshen, Leshem, Lior Fox, and Yonatan Loewenstein. “Dora the explorer: Directed outreaching reinforcement action-selection.” International Conference on Learning Representations. 2018.
[32] Jaksch, Thomas, Ronald Ortner, and Peter Auer. “Near-optimal regret bounds for reinforcement learning.” Journal of Machine Learning Research 11.Apr (2010): 1563-1600.
[33] Silver, David, et al. “Mastering the game of go without human knowledge.” Nature 550.7676 (2017): 354-359.
[34] Vinyals, Oriol, et al. “Grandmaster level in StarCraft II using multi-agent reinforcement learning.” Nature 575.7782 (2019): 350-354.
[35] Berner, Christopher, et al. “Dota 2 with Large Scale Deep Reinforcement Learning.” arXiv preprint arXiv:1912.06680 (2019).
[36] Zintgraf, Luisa, et al. “VariBAD: A Very Good Method for Bayes-Adaptive Deep RL via Meta-Learning.” International Conference on Learning Representations. 2019.
[37] Laskin, Lee, et al. “Reinforcement Learning with Augmented Data.” arXiv preprint arXiv:2004.14990 (2020).
[38] Kostrikov, Yarats and Fergus. “Image Augmentation Is All You Need: Regularizing Deep Reinforcement Learning from Pixels.” arXiv preprint arXiv:2004.13649 (2020).
[39] Pritzel, Alexander, et al. “Neural episodic control.” Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, 2017.
